All Issues
Model describes sustainable long-term recycling of saline agricultural drainage water
Publication Information
California Agriculture 57(1):24-27. https://doi.org/10.3733/ca.v057n01p24
Published January 01, 2003
PDF | Citation | Permissions
Abstract
Due to high water tables, the western San Joaquin Valley is prone to high salinity in drainage water, which requires appropriate management and disposal in order to sustain agricultural productivity. We developed a model that describes a farming system for irrigating a salt-tolerant crop with high-salinity drainage water from a salt-sensitive crop. The farming system would include the collection of subsurface drainage water from the salt-sensitive crop, which would then be combined with good, low-salinity water for an average electrical conductivity (EC) of 5 deciSiemens/meter (dS/m); irrigation of the salt-tolerant crop(s) (cotton, in this case) for several cycles; and final disposal of the drainage water in an evapor-ation pond. The main benefits of this system are that the proportion of the farm required for evaporation ponds decreases and fresh water is saved. According to our calculations, this farming system could be physically sustainable for centuries. However, the costs related to mitigating wildlife impacts caused by ecotoxic salts such as selenium in the evaporation ponds must be fully evaluated to determine the system's economic viability.
Full text
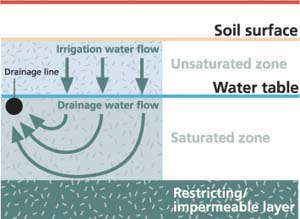
Much of the western San Joaquin Valley is plagued by high water tables, which require drainage for sustained agricultural production. The land in this area was formed from materials that in geologic time originated under the ocean, and thus contains high concentrations of chemicals associated with ocean waters. Water percolates through the crop root zone, where some is drawn into the plant via transpiration. The water that remains is more concentrated than that which was applied. It moves vertically through the unsaturated area below the root zone to the saturated zone, where soil pores are all filled with water. The water table forms the interface between these unsaturated and saturated zones. The water in the saturated zone is highly concentrated with salts, including selenium, which has ecotoxic effects to wildlife, especially birds.
In regions such as the western San Joaquin County, where water tables are high, salinity is a significant and chronic problem for agriculture. The authors modeled a system for irrigating a salt-sensitive crop such as tomatoes, above, with good-quality, low-salinity water, then recycling the drainage water through a salt-tolerant crop.
In order to effectively drain this huge subsurface “pool” of highly concentrated water, growers in the western San Joaquin Valley have developed subsurface drainage systems. These systems consist of perforated drain lines (tubes) that are buried approximately 6 feet deep and between 250 and 400 feet apart. The water flows into and through the network of tubes to a collection sump where it is pumped to the surface.
The amount of water that leaves the root zone is the same amount as enters the drain system; this water travels through pathways of variable length depending on the location where the water enters the saturated zone and the position of the drain line (fig. 1). As a result, water that originates far from the drain line has a considerably longer distance to travel than water that enters the system from directly over the drain.
Jury (1975) developed a simple mathematical model to calculate chemical concentrations in the drain, which takes into account these variable travel times. This model was used recently (Jury et al. 2003) to calculate the transition time for drainage water to reach steady state in the western San Joaquin Valley. Steady state is the point at which the concentration of salts in the water in the drain line remains the same over time. For large drain spacings typical of those found in this region, such as 400 feet, the model predicted many decades of transition time before steady state could be reached. Prior to this time, the drainage water concentrations are influenced strongly by pre-existing salinity in the saturated zone. A flushing process occurs over time, which explains why selenium continues to occur in drainage water even though essentially no selenium has been added in irrigation water applied to the soil surface.
All irrigation waters contain some dissolved salts, which become more concentrated as water is removed by the crop via transpiration. The ratio of drainage volume to irrigation volume is called the leaching fraction, which is approximately equal to the ratio of the irrigation water's salinity to the drainage water's salinity in steady state. In the western San Joaquin Valley the concentration of irrigation water is low enough that for typical leaching fractions, the salinity of water leaving the root zone is less than that of the resident groundwater being displaced. In general, more salts are removed in the drainage water than are being applied with irrigation water. As a result, some of the salts stored in groundwater originating from geologic times are mined through the drainage process.
One option for disposing of drainage water is to reuse it on salt-tolerant crops. For this type of operation, however, the water percolating below the root zone would be very high in salinity because of the initial high salinity of the applied water and the concentrating effects of water removal by the plant. In this case, the concentration leaving the root zone would be higher than the resident groundwater, so that salts would be stored in groundwater.
The combination of irrigating salt-sensitive crops with good-quality (low salinity) irrigation water and then irrigating salt-tolerant crops with the resulting drainage water creates a cyclic process in which salts are first extracted from groundwater and subsequently recharged to it. However, since there is a continual input of salts to the valley through imported irrigation water, salts gradually accumulate in the system and eventually must be disposed of in some manner.
We simulated the long-term consequences of a farm system that included irrigating salt-sensitive crops with good-quality water (EC [electrical conductivity] = 0.6 deciSiemens/meter [dS/m], a standard measure of water salinity), followed by irrigating salt-tolerant crops with a blend of drainage and good waters, and eventually using an evaporation pond for ultimate disposal of the salts. The imposed conditions, typical of normal farm operations, included planting only economic crops and restricting yield reductions to less than 10%.
Simulation conditions
Water leaving the root zone at a location a short distance from the drain reaches the place of removal in a relatively short time, whereas it may take considerably longer (several years) for water originating at greater horizontal distances from the drainage line to arrive (fig. 1). As a result, at any given time following the start of an irrigation operation on a field overlying saline groundwater, the drain will contain a mixture of water originating from the irrigation and resident groundwater. Using the Jury (1975) method, it is possible to calculate the fraction of water in each category removed by the drain as a function of time.
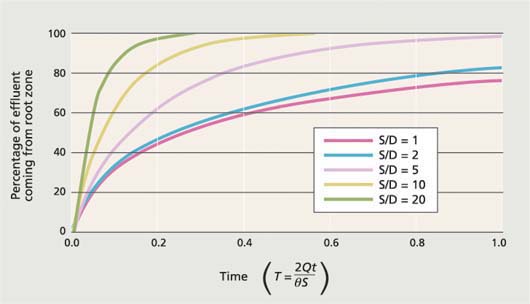
The percentage of water collected in the drainage system that comes from the root zone can be expressed as a function of a term (T) where T = 2Qt/θS, and Q is deep percolation in acre-feet/acre/year, S is drain spacing in feet, θ is the saturated water content of the soil, and t is the time in years (fig. 2). This relationship depends upon the ratio of drain spacing (S) and depth (D) to an impermeable/restricting layer. Note that it can take a number of years before the water collected in the drain line originates entirely from the root zone. For example, if S = 400 feet, Q = 1 foot/year, θ = 0.5 and T = 1, then t = 100 years. The time increases with the drain-line spacing and/or depth to the impermeable layer.
Fig. 1. Irrigation water flows vertically from the soil surface through the unsaturated zone and then moves horizontally through the saturated zone toward the drainage line.
Fig. 2. Percentage of drain effluent collected in the drainage system that comes from the root zone; this relationship depends upon the ratio of drain spacing (S) and depth (D) to an impermeable layer. T = 2Qt/θS, where Q = deep percolation (acre-feet/acre/year), S = drain spacing (feet), θ = saturated water content of soil, and t = actual time in years.
Because the Corcoran clay layer — the restricting layer — is very deep compared to the region's typical drain spacing, our computations were done for the curve where S/D = 1. The Jury et al. (2003) model makes a number of simplifying assumptions, including neglecting groundwater movement. However, the effect of moving groundwater, if any, would be to decrease the amount of drainage water in the drain compared to resident storage, delaying the time needed to reach steady state indefinitely. Neglecting its effect is therefore conservative. Other influences such as the spatial variability of soil properties are site specific; but, if random they would not affect travel paths appreciably.
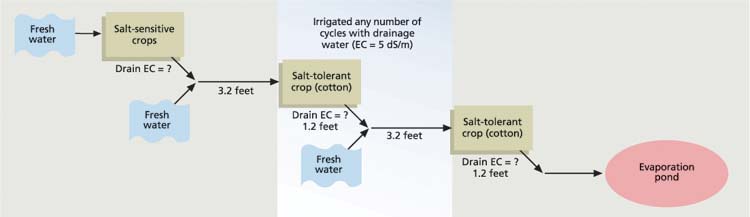
Fig. 3. A model drainage-water reuse system for economically productive crops (EC = electrical conductivity).
The salinity of drainage waters in the valley typically creates an EC approximately equal to 10 dS/m. We assumed that the drainage water initially collected from the salt-sensitive crop would be at this concentration. Since irrigation water salinity of 10 dS/m is very high for irrigating cotton, our simulation assumed that drainage water and good water would be combined to an average of 5 dS/m. For this analysis, we relied on Letey and Dinar (1986) for the relationships between cotton lint yield and the amount of water applied at various irrigation water salinities. Furthermore, the uniformity of irrigation affects the relationship between yield and the amount of applied water (Letey et al. 1984). We assumed a Christiansen's uniformity coefficient (CUC) equal to 70, which is typical for a furrow irrigation system. We also assumed that the cotton irrigation would produce a lint yield equal to 92% of maximum potential yield. These conditions specified that a total of 3.2 feet of water would be applied, resulting in 1.2 feet of deep percolation (fig. 3).
We assumed two irrigation management cases for the salt-sensitive crop area. One produced 8.8 inches per year of drainage water, and the second imposed a high level of irrigation management that resulted in 4.4 inches per year of drainage water. The EC of the water collected in the drainage system was computed each year using the travel time information in figures 1 and 2. The EC of the drainage water from the salt-sensitive crop area would decrease with time because the salinity of the water leaving the root zone would be less than the resident groundwater's salinity.
The EC of the water collected in the drainage system would dictate how much good-quality water should be used to achieve an average of 5 dS/m irrigation water for cotton. Rainfall that did not evaporate during the winter would provide a fraction of the “good quality” water. As the EC of the drainage water decreased, the required amount of good water decreased. The EC of the drainage water from cotton was calculated yearly. In this case it increased with time, and relatively more good water was required to achieve the average 5 dS/m water. The analyses were done for various numbers of reuse cycles on cotton before the drainage water was disposed of in an evaporation pond.
Irrigation management practices
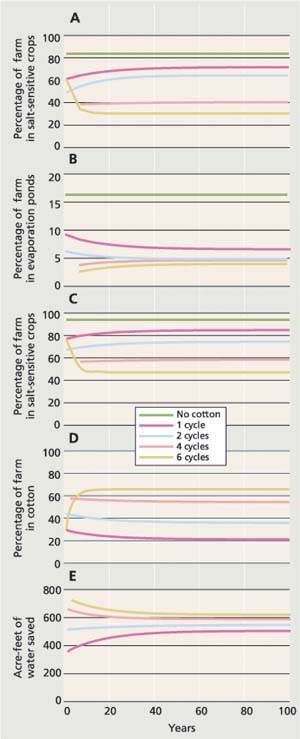
We calculated the percentage of the farm that could be retained in salt-sensitive crops — such as tomatoes — for up to 100 years, when the drainage volume from the salt-sensitive area is 8.8 inches per year at various numbers of times that it is recycled through cotton (fig. 4A). Increasing the number of cycles decreases the fraction of the farm that can be retained in salt-sensitive crops. However, cycling the drainage water through cotton also decreases the percentage of the farm that must be devoted to evaporation ponds (fig. 4B). We assumed that evaporation from the ponds was 4 feet per year.
Imposing good irrigation management that reduces drainage volume to 4.4 inches per year increases the percentage of the farm that can be planted in salt-sensitive crops (fig. 4C). When compared with drainage of 8.8 inches per year (fig. 4A), decreasing the drainage volume from the salt-sensitive crop area also reduces the percentage of the farm that must be devoted to evaporation ponds (data not shown).
As expected, increasing the number of reuse cycles increases the percentage of the farm that must be devoted to cotton, at 8.8 inches per year of drainage water from the salt-sensitive crop area (fig. 4D). If the drainage water from the salt-sensitive crops is reduced, the percentage of the farm devoted to cotton could also be reduced.
A system employing furrow irrigation of salt-tolerant cotton, above, with a combination of saline drainage water and fresh water could theoretically be sustainable for many decades. However, the costs of disposing salts accumulated in evaporation ponds and related wildlife impacts must be carefully considered.
Cotton is a common crop in the western San Joaquin Valley and is usually irrigated with good-quality water. In our scenarios, drainage water was partially used to irrigate the cotton. Therefore, we computed the difference in the amount of good water that would be used for cotton with and without blending in drainage water. The difference between these two numbers is considered the amount of fresh water saved by using the drainage water. On a 1,235-acre farm, the increase in acre-feet of fresh water saved by increasing the number of cycles is partially attributed to the fact that more land was also farmed to cotton (fig. 4E).
There are two benefits to recycling drainage water through cotton: the percentage of the farm required for evaporation ponds decreases and fresh water is saved. The monetary value of the water saved depends upon whether the returns are simply associated with applying less fresh water or whether the fresh water can be marketed and sold to the urban sector, where its value is greater. If this is possible, cycling drainage water through cotton could produce significant revenue to offset some of the costs associated with total farm operations.
Long-term system sustainability
The results of this simulation indicate that a system which irrigates salt-sensitive crops with good-quality irrigation water and reuses the drainage water to partially supply water for a salt-tolerant crop, with eventual disposal into an evaporation pond, can be physically sustained for centuries in the western San Joaquin Valley. Management to reduce drainage volumes from the salt-sensitive crop area has a high payoff, in that it allows a greater percentage of the farm to be maintained in salt-sensitive crops and a lower proportion to be devoted to evaporation ponds. Although cotton was selected for this analysis, any salt-tolerant crop could be substituted.
A critical feature of this operation is that evaporation ponds are necessary to ultimately dispose of accumulating salts. It is possible to utilize solar evaporator ponds, in which the drainage water is discharged at rates equal to or less than the evaporation rate. We know of no other option for disposing salts on farmland while maintaining high crop productivity on the major part of the farm. Because of selenium in drainage water, evaporation ponds must also be managed to mitigate wildlife hazards. This may require netting the ponds and/or a combination of management and compensation habitat. The costs associated with the mitigation procedures depend on the extent to which they are required. Therefore, although this system is physically sustainable for centuries, its economic sustainability must still be evaluated.
Fig. 4. Over a 100-year period for various numbers of times drainage water is cycled through salt-tolerant crops, the percentage of a model cotton farm with furrow irrigation that could be retained in (A) salt-sensitive crops (with drainage volume of 8.8 inches/year), (B) evaporation ponds (drainage volume, 8.8 inches/year), (C) salt-sensitive crops (drainage volume, 4.4 inches/year), or (D) cotton (drainage volume, 8.8 inches/year), as well as (E) amount of fresh water saved (drainage volume, 8.8 inches/year).
In areas where the selenium concentration in drainage water is particularly high, the selenium concentration in the evaporation pond could exceed the level established for classifying water as a toxic waste, greatly increasing costs and perhaps making the system economically unfeasible. The criteria used to classify selenium-tainted water as toxic waste play a critical role in future opportunities to maintain agricultural production in a sustainable manner without out-of-valley disposal of drainage waters.
The current soluble threshold limit concentration (STLC) for classifying selenium as toxic waste is 1.0 mg/L. This STLC was derived by multiplying the California drinking water standard for selenium by an environmental accumulation factor of 100. The California drinking water standard was 10 mg/L in the early 1980s when the hazardous waste limits were adopted. The drinking water standard has since been changed to 50 mg/L, but the STLC was not adjusted.
Since wildlife must be protected at concentrations that are orders of magnitude less than the STLC, raising the STLC would have no impact on hazards to wildlife. Indeed, increasing the legally defined STLC would have an insignificant impact on environmental hazards but would facilitate opportunities to maintain an economically sustainable agriculture production system in the western San Joaquin Valley.