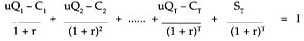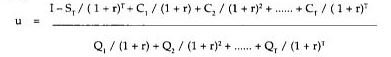All Issues
“New” method simplifies decision of when to replace orchards
Publication Information
California Agriculture 53(3):30-32. https://doi.org/10.3733/ca.v053n03p30
Published May 01, 1999
PDF | Citation | Permissions
Abstract
This article presents a “new” method for making decisions on when to replace depreciable assets. The method is simpler than other standard methods because it uses only known cost data, avoiding the problems of using price forecasts. An application to cling peach orchards is given to explain and illustrate the method.
Full text
Managers frequently face decisions about when to replace depreciable assets, but it is a controversial topic. The basic problem is that all of the standard methods in use require a forecast of the price of the output that is produced while using the asset, unless output is constant and unaffected by age of the asset. For example, in the case of a peach orchard, the usual discounted cash flow methods require a forecast of peach prices for each year over the expected life of the trees. Controversy arises over the validity of price forecasts, no matter how those forecasts are made.
The “new” method presented here avoids this problem by not using price forecasts, instead using only known historical cost data. The method can be attributed to a largely overlooked 1925 article by Harold Hotelling, a famous statistician and economist. The criterion for replacement is “minimum unit cost.” In other words, the age of replacement is chosen so as to minimize the cost of production per unit of output. An application to cling peach orchards is given here to explain and illustrate the method, as well as to provide specific information to peach growers. Sequential fine tuning of the replacement decision in the face of price uncertainty is also discussed.
Replacement decision method
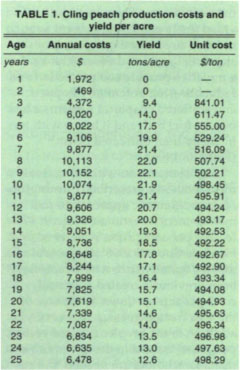
All replacement decision methods begin by evaluating the expected productivity of an asset over its life. The typical yield pattern by age of trees for late-maturing peach varieties is given in the third column of table 1, which was constructed from data in the California Cling Peach Advisory Board Orchard Production Survey, 1994–95. Yields are zero the first 2 years after planting and then increase steadily, reaching a maximum of 22 tons at age 9, when yields start declining steadily to about 12.5 tons by age 25. Initial establishment of the orchard requires quite a large outlay, which is followed by 2 years without revenue and some additional costs before revenues begin, making peach production a long-term, capital-intensive investment. An important economic question is: What is the optimal age at which the orchard should be replaced, or the land devoted to another use? This question is answered by applying Hotelling's minimum unit cost criterion.
Investing land and capital in the production of an orchard crop is intended to generate a cash flow from that crop. A large part of the total cost of the investment is the interest expense associated with the money tied up in land and capital. The primary nonland investment is establishment costs incurred before the trees begin to bear fruit. Cash flow costs are annual outlays associated with caring for the trees, cultural costs and harvest costs. The general idea behind the unit cost criterion for replacement is to calculate the cost per unit of output (peaches in this example) for a given replacement age and, through a search over various replacement ages, to choose the age that has the smallest cost associated with it. If all costs were taken into account (including those that do not affect optimal replacement age, such as fixed costs and management), a price per unit of output just equal to this minimum cost, referred to as “unit cost,” would allow the firm to break even in the production of peaches. The objective is to choose the replacement age that minimizes the cost per unit of output to obtain the largest profit margin.
The value of land is treated as the initial investment cost, and this cost is recovered at the end of the orchard's economic life. Establishment costs for the orchard are put into the first year's annual cost category. Establishment costs could be included with land value, but then their depreciated value of zero at replacement would need to be recognized. Salvage value of the orchard investment is the net market value of the old trees, which could be either positive or negative, plus the value of land which, with few exceptions, would suffer no depreciation over the life of the orchard.
It is necessary to define some special notation in order to make the definition of the minimum unit cost criterion for replacement unambiguous. In the following definitions, the subscript j on a letter denotes the jth year in the life of the asset:
Cj = annual cost associated with an asset of age j
Qj = quantity of output from the asset at age j
T = replacement age
I = initial investment cost of the asset
ST = salvage value of the investment if replaced at age T
r = real rate of interest expressed in decimal form (nominal rate minus the inflation rate)
u = cost per unit of output from the asset
A dollar value received t years in the future is transformed into an amount that is comparable to a dollar received now by dividing the future amount by (1 + r)t. For example, with an interest rate of 5%, $10 received 2 years from now would at present be worth $10/(1 + r)(1 + r) = $10/(1.05)2 = $9.07. The unit cost equation described earlier can be written as Equation 1 (see box below).
Except for the last term, which is salvage value, each term on the left side of the equal sign represents a year in the life of the orchard, where the exponent on (1 + r) is the age of the orchard, or the number of years for which the cash flow must be discounted to be comparable to the year the orchard was planted. Consequently the terms on the left, and the initial investment cost on the right, are dollar measures adjusted to the same point in time, which provides a valid equation to calculate the cost per unit of production.
Solution of the equation for the unit cost variable u yields the formula designated as Equation 2 (see box).
One obtains the minimum unit cost replacement age by searching over a set of values for T that is expected to include the optimal replacement age, and the smallest value of u indicates the optimal choice of T. Programming the calculation of u, for example with spreadsheet software, is simplified by the simple structure of the numerator and denominator. As replacement age is increased by 1 year, two new terms are added, one each to the numerator and the denominator, and the previous salvage value term in the numerator is divided by (1 + r). Therefore a simple computational program would be oriented around these three variables, which are updated at each iteration, where an iteration adds 1 more year to the life of the orchard. In fact, the computations would be quite feasible using a hand-held calculator. The following example illustrates the general application of this replacement criterion for a cling peach orchard.
Cling peach orchard replacement
Estimates of the costs and physical relationships summarized earlier were made for a small peach orchard in the southern San Joaquin Valley. Estimates of annual costs (C) and peach yields (Q) in relation to the age of the orchard are given in table 1. Salvage value of the orchard itself (excluding land) is approximated as zero. Therefore salvage value S(T) in the formula for unit cost is the value of land at the time of replacement, which is taken to be equal to $5,500 per acre, the same value used for the investment cost of land at the time the initial orchard is planted. The real rate of interest used is 5%. This is all the data that is needed to apply the unit cost criterion to optimal replacement of the peach orchard.
The lowest cost of producing a ton of peaches is achieved with replacement at 15 years (table 1), and this result does not change if land value is between $2,000 and $10,000 per acre. With land price at $500 to just under $2,000 per acre, the optimal replacement age is 14 years, while a land value of $25,000 calls for replacement at 18 years. The economic intuition underlying this result is that the high interest costs accompanied by low yields early in the yield cycle must be compensated by holding the orchard longer, even though yields are decreasing considerably between ages 15 and 18. Modest changes in the salvage value of the old orchard, up or down by $500, did not alter the replacement age from 15 years.
Optimal replacement age was quite insensitive to changes in the interest Equation 1Equation 2 rate; replacement age remained constant at 15 years when the rate varied from 2% to 9%. This interval includes the normal range of real interest rate, that is, rates corrected downward for the prevailing rate of inflation. Of course, unit cost over the same interval for interest rates increased steadily, from $479 to $513 per ton. Replacement age drops to 14 years for rates less than 2%. Incidentally, a zero interest rate in the formula for unit cost converts the unit cost formula into average cost per unit of output, which is quite an intuitive criterion when the business does not have to bear any interest costs, either explicit or implicit, through opportunity cost of the firm's own funds.
Although the optimal replacement age is changed by altering the interest rate and other economic factors involved in unit cost measurement, replacing the orchard 3 years too early or late increases the cost per ton of peaches by only a dollar or two (see the last column in table 1). Mistakes in the direction of too short a period are more costly than keeping the orchard too long. For example, replacing the orchard after 25 years (a 10-year error) gives a cost of $498 per ton instead of the minimum of $492, while replacement at age 10 (a 5-year error) gives the same cost of $498 per ton. Since the unit cost of peach production is so insensitive to modest variations in replacement age around that estimated here, peach producers should feel comfortable using 15 years as a “rule of thumb” replacement age for their orchards.
These results also suggest that the risk involved with respect to getting locked into a long-lived perennial crop, when it is cling peaches, is not as great as one might expect. If the orchard were removed after only 7 years, unit cost would be $516 instead of the minimum of $492 at 15 years, which is only a 1% sacrifice. This difference in cost seems small in comparison with year-to-year variations in peach prices that are commonly observed.
The insensitivity of unit cost to delaying the replacement age of a peach orchard by as much as even 10 years from the least-cost age provides the producer great flexibility to delay replacement if peach price expectations are relatively high for the near future. Replacement of peach trees results in almost zero production for 3 years, making it economically attractive to postpone replacement until price expectations decline to what is thought of as more nearly normal levels. This observation also suggests that a risk-averse producer would be inclined to diversify by synchronizing various aged stands to provide a fairly constant total supply of fruit. Nevertheless, the astute producer would probably deviate from the nearly even aged stands goal to exploit short-run output price dynamics. Data on aggregate acreage response to changing prices by cling peach growers suggest a tendency to diversify by avoiding heavy concentrations of trees of the same age.
Other uses of the method
The unit cost method for determining the economic replacement of assets that was applied here to peach orchards is also applicable to other assets, such as farm machinery and other long-lived assets. However, the proper unit to use for output is often ambiguous in other applications One might use acres harvested, quantity of production harvested or hours of a standardized service performed as the unit of output from equipment such as a grain or tomato harvester. If such a machine were used in a custom farming business, it would seem that the best choice of unit would be that which is used for pricing the services provided. For example, if one charges by the acre for harvesting, that would suggest acres as the unit of service on which one would want to minimize the unit cost with respect to replacement age.
It is important to recognize that the method outlined for the peach orchard does not allow for random events that often affect the economic life of an asset, such as mechanical failure of a major component in a machine that would require expensive repairs to make it operational again, or a certain amount of obsolescence associated with technological change. Hotelling addressed the latter problem by specifying unit cost with a downward sloping trend to capture the gradually falling cost of a standardized unit of service from the machine caused by gradual technical improvements.
The complication of random failure of a machine with major repair costs required to make it operational again can be handled to some extent by making two estimates of the cost per unit of service: (1) unit cost associated with buying a new machine and accepting the salvage value for the old, and (2) unit cost associated with repairing the old machine and keeping it for an estimated optimal economic life, given the condition in which it will be after the repairs. Conceptually this approach appears quite straightforward, but the big challenge is estimating the empirical relationships involved; for example, future costs and physical output of services from the old machine after it has been repaired. Nevertheless, it is often helpful to have a clear concept of the proper criterion to use in struggling with these types of decisions when limited data is available to approach the problem in a formal way.
In summary, the method described here for use in making replacement decisions is usually simpler than most methods in use currently and can be applied in any circumstance. The simplification comes from not having to forecast future prices or values of an output or service associated with the asset. In fact, the economic replacement framework described here provides the basis for estimating the cost per unit of output from an orchard crop, or the cost per unit of a standardized unit of service from a machine such as a tomato or grain harvester.